|
You should be familiar with the concept of a directed graph (or digraph) from MATH 142 and earlier discussions in CMPS 144. To remind you, a digraph is composed of nodes (or vertices) and edges. Each edge is an ordered pair (u,v) of nodes. We say that this edge emanates from u and goes to v. In a diagram that depicts a digraph (as seen below), the nodes are usually shown as ovals or boxes and an edge (u,v) is shown as an arrow directed from node u to node v. For the purposes of this assignment, we will assume (contrary to convention) that a digraph can include self-loops, which are edges going from a node to itself.
A path in a digraph is a sequence of nodes <v1, v2, ..., vn> such that, for each i, 1≤i<n, (vi, vi+1) is an edge in the digraph. The length of this path is n−1, as that's how many edge "traversals" would be necessary to follow it to completion. If there is a path from node u to node v, we say that u reaches v. A special case of a path is a cycle, which is a path of non-zero length that begins and ends at the same node but in which no other node appears twice. (Thus, a self-loop is a cycle of length one.)
The outdegree of a node is the number of edges emanating from it and the indegree of a node is the number of edges going to it. Here we shall be concerned specifically with digraphs in which every node has outdegree one. We call such a graph an outdegree-1 graph.
Outdegree-1 graphs have the property that, for every node v and every natural number k, there is a unique path of length k starting at node v. We use destination(v,k) to refer to the node at the end of that path. (Indeed, the only interesting method in GraphOutDeg1 is destination(), which implements this function.)
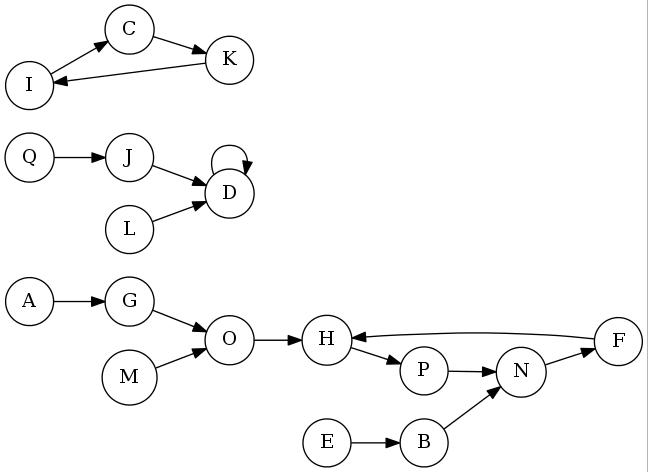
Another property of outdegree-1 graphs is that, from every node, some cycle is reachable. An example outdegree-1 graph is pictured below. Notice that such a graph may have multiple components, each one comprising all the nodes that lie on a particular cycle, plus all the nodes from which that cycle can be reached.

|
Provided to you are the following:
The data in each file has a format exemplified by
7 4 2 0 2 5 1 5 |
This sequence of numbers describes a graph of seven nodes (as indicated by the first number) in which the edges emanating from nodes 0, 1, ..., 6 go to, respectively, nodes 4, 2, 0, 2, 5, 1, and 5.
The student's task is to complete the Java class OutDeg1GraphPlus, which augments its parent class, OutDeg1Graph, by introducing some new observer methods.
The specifications of the new observer methods are as follows:
/* Reports whether or not nodes v and w are ** in the same component of this graph. */ public boolean inSameComponent(int v, int w) /* Returns the length of the shortest path from ** node v that reaches a node that lies on a cycle. */ public int distanceToCycle(int v) /* Reports whether or not node v lies on a cycle. */ public boolean onCycle(int v) /* Returns the number of components in this graph. */ public int numComponents() |
public boolean onCycle(int v) {
final int N = numNodes();
int k = 0;
int w;
do {
k = k+1;
w = destination(v,k)
}
while (v != w && k != N);
return v == w;
}
|
Here we shall take the attitude that it is worth using some extra memory if the resulting benefit is that our methods can be made to run more quickly (because multiple executions of those methods need not repeat the same work multiple times). That attitude has led us to declare three instance variables in GraphOutDeg1Plus, namely rep[], distToCycle[] (both arrays), and numComponents, as well as an extremely valuable utility method, resolve().
The idea underlying rep[] is that each component in the graph should have one node that is deemed to be its representative. For node v, the value of rep[v] —once it has been computed and stored there— identifies the node that is the representative of the component in which node v lies. Assuming that both rep[v] and rep[w] have been computed, it is then very easy to determine whether nodes v and w are in the same component (which is the question answered by the call inSameComponent(v,w)).
As for distToCycle[], the obvious intent is for it to be used by the distanceToCycle() method, so that, even if a client program asks for node v's distance to a cycle multiple times, that value need be computed only once.
The intent of the resolve() method is that, for the node v provided to it via its formal parameter, it should perform whatever work is needed to compute the correct values of rep[v] and distToCycle[v] (and, of course, to store those values in those places!). We say that node v has been resolved if rep[v] and distToCycle[v] have been computed.
If designed well, the work carried out by resolve() in resolving node v need not be repeated when resolving some other node w. Indeed, a well-designed version of resolve() will, as a result of resolving node v, also resolve every as-yet-unresolved node w that is reachable from v.
Choose vk to be the representative of the component that includes all the nodes on the stack. Repeatedly pop those nodes until vj has been popped. For each such node, place the correct values into its rep[] and distToCycle[] array elements, namely vk and zero, respectively.
The remaining nodes on the stack (if any), going from top to bottom, are vj-1, vj-2, ..., v0. Pop each of them and place the correct values into their respective rep[] and distToCycle[] array elements. For the former, that would be vk. For the latter, those values would be, respectively, 1, 2, ..., j (as the distance to vj from each of those vi's is j−i).
To carry out the algorithm described above, you need to be able to tell, for a given node, whether it is on the stack. How can this be done? One nice way would be to make use of the rep[] array. By looking at the constructor, you can see that all its elements are initialized to −1. When a node gets pushed onto the stack, you can record that information by replacing its value in rep[] with, say, −2. In effect, then, there are three cases:
To simplify the description of the algorithm above we assumed that, when resolving node v, none of the nodes reachable from v already had been resolved. Let's no longer make that assumption. What could happen, then, when pushing nodes v0, v1, v2, etc., onto the stack is that we could encounter node vk that has already been resolved. (Recall that we can use rep[w] to determine whether or not node w has been resolved.) In that case, pop all the nodes (namely, vk-1, vk-2, ..., v0) from the stack and, for each one, make its representative be the same as vk's representative. For each such node vi, record its distance to a cycle as being k−i more than vk's distance to a cycle.
One way to design these methods, then, would be to assume, for each one, that all nodes in the graph already had been resolved. Indeed, that could be a precondition of each method. To insure that this precondition was met, the constructor could invoke the resolve() method upon every node in the graph! That way, once the constructor had terminated, every node would have been resolved!
However, that would be a sub-optimal design. Why? Because it is not at all far-fetched to expect a client program to create a (large) graph and then to ask questions about it (via calls to the observer methods) that require only a relatively small percentage of its nodes to be resolved. In that case, it would be wasteful to have resolved all the nodes.
The suggestion being given here, then, is that the observer methods under discussion should first check to see whether the node(s) relevant to it have been resolved. If not, resolve it/them; otherwise, skip that step. Then use the relevant array elements (in either rep[] or distToCycle[]) to formulate the correct response.