Prim's Algorithm takes as input a connected undirected graph G each of whose edges has an associated cost and produces as output a subgraph T of G that is a minimum spanning tree (MST) of G. That is, T is a tree (i.e., an acyclic connected graph) that includes all the vertices of G (hence, it "spans" G) together with a subset of G's edges whose total cost is minimum among all spanning trees of G. If G is not connected, applying Prim's Algorithm to each of G's connected components1 yields a minimum spanning forest2 of G, each of whose trees is a minimum spanning tree of one of G's connected components.
Prim's algorithm is an example of a greedy algorithm, meaning one that, at each step, "makes a choice" that appears to be best, given the current situation. Due to the nature of the problem under discussion, this greedy approach works. For some problems, making what appears to be the best choice at the moment does not lead to an optimum solution.
The underlying reason for why a greedy approach works in choosing a set of edges that forms an MST of a graph is embodied in this theorem:
Theorem: Let G = (V,E) (V is the set of vertices, E the set of edges) be a connected graph (whose edges have associated costs). Suppose that S is a proper subset of V and let e be a minimum-cost edge among the edges having one endpoint in S and the other in V−S. Then edge e is in a MST of G. Note: This theorem is not quite stated correctly. A better version will appear later.
As a consequence, an algorithm attempting to construct a MST of a graph by repeatedly choosing edges to be included in that tree cannot "go wrong" by choosing an edge of minimum cost that connects two vertices that are not connected by any path using previously chosen edges.
The way that Prim's algorithm works is that it maintains a partial MST T = (S,E') of the given graph G = (V,E). It begins with S = {v} and E' = ∅ for some arbitrarily chosen vertex v. At each step, a minimum-cost edge {x,y} among those having one endpoint in S (x, say) and the other (y) in V−S is chosen to be included in the MST. That is, S is enlarged to include vertex y and E' is enlarged to include edge {x,y}.
At a high level of abstraction, the algorithm goes like this:
|
// Input: G = (V,E) (V is a set of vertices, E ⊆ V×V
is a set of edges) // Precondition: G is connected (i.e., for every pair of vertices, there is a path that connects them) // Output: T = (V,E'), a mimimum spanning tree of G v := any member of V
S := {v} // S = set of vertices already included in T
E':= ∅ // E' = set of edges already included in T
// Loop invariant: T' = (S,E') is a minimum spanning tree of the
// subgraph of G induced by S.
while S ≠ V {
Identify edge {x,y}∈E of minimum cost such that x∈S and y∈V−S
S := S + y
E':= E' + {x,y}
}
|
Refining the first step in the loop body, we get the following algorithm, which has a bit of a "brute force" flavor about it:
v := any member of V
S := {v} // S = set of vertices already included in T
E':= ∅ // E' = set of edges already included in T
// Loop invariant: T' = (S,E') is a minimum spanning tree of the
// subgraph of G induced by S.
while S ≠ V {
minCostSoFar := maximum of set {cost(e) | e∈E } // or any larger value
for each edge {x,y}∈E such that x∈S ∧ y∈V-S {
if (cost({x,y}) < minCostSoFar) {
minCostSoFar := cost({x,y})
u := x; w := y;
}
}
// assertion: u∈S ∧ w∈V−S ∧ {u,w} has minimum cost
// among edges connecting vertices in S and V−S
S := S + w
E':= E' + {u,w}
}
|
Analysis: Let |V| = n and |E| = m. The outer loop iterates exactly n−1 times, each time placing one more vertex into S. During each iteration of the outer loop, the nested loop iterates m times, once for each edge. Thus, the nested loop iterates a total of m(n−1) times. If we assume that each of the expressions representing set membership test (e.g., x∈S, y∈V−S) can be evaluated in constant time, then what we have is an algorithm whose running time is O(m·n). Unless G is a relatively sparse graph, m is proportional to n2, and so this translates to O(n3).
Perhaps we can improve upon this. A good place to start is by asking this question:
Is it really necessary to examine every edge in the graph in order to identify the next edge that ought to be placed into T?
It turns out that the answer is no. Indeed, we can improve upon this running time significantly by maintaining a set/list of those vertices that are not in S but that are connected by an edge to at least one vertex in S. Those, after all, are the only vertices that are candidates to become members of S on the next iteration of the outer loop. Let's refer to the set of such vertices as Z. In addition to simply keeping track of which vertices are in Z, we should also remember, for each such vertex, which edge connecting it to a vertex in S has minimum cost.
Using these ideas, we refine the algorithm to the following:
v := any member of V
S := {v} // S = set of vertices already included in T
E':= ∅ // E' = set of edges already included in T
Z := ∅ // Z = set of vertices not in S but adjacent to some vertex in S
for each w∈V such that {v,w} is an edge {
Z := Z + w // Place neighbors of v into Z and record that each one's
closest[w] = v // min-cost connection to S is via its edge to v.
}
// Loop invariant:
// T' = (S,E') is a minimum spanning tree of the subgraph of G induced by S ∧
// Z includes all vertices not in S but adjacent to some vertex in S ∧
// for all y in Z, closest[y] = x means that x∈S and {x,y} has minimum cost
// among edges connecting y to a vertex in S.
while S ≠ V { // or, equivalently, Z ≠ ∅
x := member of Z such that cost({closest[x],x}) is minimum
Z := Z - x
S := S + x
E':= E' + {closest[x],x}
for each y such that {x,y}∈E {
if y∈S {
// do nothing
}
else if y∈Z {
if cost({x,y}) < cost({closest[y],y}) {
closest[y] = x
}
}
else { // y ∈ V - (S ∪ Z)
Z := Z + y
closest[y] = x
}
}
}
|

|
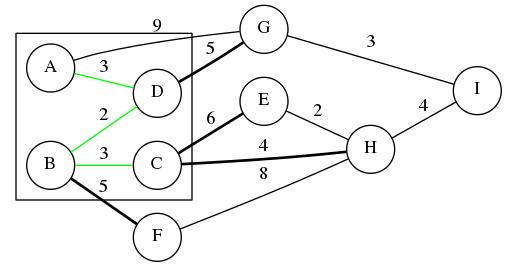
For each vertex in Z, the minimum-cost edge connecting it to a member of S is shown with a thick line. These are the only edges that are candidates to be inclued in the MST during the next loop iteration. (Notice that edge {A,G} is not thick because edge {D,G} has lower cost.) Now, the minimum-cost edge among these is {C,H}, with a cost of 4. Thus, on the next loop iteration, vertex H will be placed into the MST (i.e., by "transferring" it from Z to S) and edge {C,H} will be placed into the tree (i.e., by putting it into E').
In order to maintain the invariant of the outer loop, it will also be necessary to place into Z all those vertices to which H has an edge and which are currently in neither S nor Z. Moreover, elements of the closest[] array corresponding to these vertices must be filled by the costs of their edges to H. Finally, it may be necessary to make reductions to elements of the closest[] array corresponding to vertices in Z to which H has an edge.
There are three edges incident to H:
Analysis: Every vertex is placed into S exactly once. Immediately thereafter, its set of edges is iterated over by a for-loop. Assuming that that iteration takes time proportional to the number of edges in that set (which is realistic if adjacency lists are used in the representation of the graph), the total running time for the two for-loops is O(n+m). If, however, iterating over a vertex's edge set takes time proportional to n (the number of vertices), as would be the case if an adjacency matrix were being used to represent the graph, the running time would be O(n2).
As for the while-loop, it iterates n−1 times, each time transferring one vertex from Z into S. Aside from the for-loop nested inside it, which we have already accounted for, what is clearly the most expensive operation is the one that determines the vertex x to be taken from Z and placed into S. In the worst case, that should take no more than time proportional to n. As it will be carried out n−1 times, that gives a total of O(n2) time.
The conclusion is that the 2nd refinement of Prim's algorithm reduces its running time to O(n+m + n2), which simplifies to O(n2) (because m is at most O(n2)), compared to the previous version's O(n·m), which, in the not unusual case that m is O(n2), simplifies to O(n3).
Subprogram PrimOneComponent(v):
///////////////////
S := {v} // S = set of vertices already known to be in v's component
E':= ∅ // E' = set of edges already included in T
Z := ∅ // Z = set of vertices not in S but adjacent to some vertex in S
for each w∈V such that {v,w} is an edge {
Z := Z + w // Place neighbors of v into Z and record that each one's
closest[w] = v // min-cost connection to S is via its edge to v.
}
// Loop invariant:
// T' = (S,E') is a minimum spanning tree of the subgraph of G induced by S ∧
// Z includes all vertices not in S but adjacent to some vertex in S ∧
// for all y in Z, closest[y] = x means that x∈S and {x,y} has minimum cost
// among edges connecting y to a vertex in S.
while Z ≠ ∅ {
x := member of Z such that cost({closest[x],x}) is minimum
Z := Z - x
S := S + x
E':= E' + {closest[x],x}
for each y such that {x,y}∈E {
if y∈S {
// do nothing
}
else if y∈Z {
if cost({x,y}) < cost({closest[y],y}) {
closest[y] = x
}
}
else { // y ∈ V - (S ∪ Z)
Z := Z + y
closest[y] = x
}
}
}
return (S,E')
|
Notice that the while loop's original guard, S ≠ V, has been replaced by Z ≠ ∅, reflecting the fact, when Z has become empty, it must be that every vertex in v's connected component has been placed into S, implying that the computation of a minimum spanning tree of that component is complete. The loop guard S ≠ V will not work when G is disconnected, because S can never include vertices from a connected component that does not include vertex v. (In other words, S ≠ V works as a loop guard only if G is a connected graph.)
To obtain a minimum spanning forest F = (V, EF), we can execute this algorithm:
SF := ∅
EF := ∅
for each vertex v ∈ V {
if !(v ∈ SF) {
S,E := PrimOneComponent(v)
SF, EF := SF + S, EF + E
}
}
|
Upon completion of execution, we will have SF = V (the vertex set of G) and F = (V, EF) will be a minimum spanning forest of G. As for the runtime complexity of this algorithm, even though it calls PrimOneComponent() up to n times (once for each vertex of G), its asymptotic running time is the same as we calculated for PrimOneComponent() itself, O(n2).
Why? Consider that the operations that dominate the running time of the algorithm are those required in carrying out
Taken over all calls to PrimOneComponent(), each vertex in G will be the target of assignment (1) exactly once. Which is to say that assignment (1) will be executed exactly n times. Each time it occurs, it should take no more than O(n) time, because, in the worst case, iterating through all n vertices (to check the value of cost(closest[z],z) for all z∈Z) should be doable in linear time. Thus, the total running time for (1) is O(n2).
The loop (2), taken over all calls to PrimOneComponent(), will be executed exactly n times (once for each vertex in G), for the reasons described above. Each execution of the loop should take time O(n) in the worst case, enough to identify each neighbor y of vertex x and to carry out the appropriate operation upon y (in accord with the three-branch if-else statement). Thus, the total running time for (2) is O(n2).