In Chapter 3 of the Linz text, it was shown that the class of languages that can be described by finite automata (either deterministic or nondeterministic), regular expressions, and both right-linear and left-linear grammars are all the same. In other words, any language that can be described by, for example, an NFA can also be described by a regular expression, and vice versa. This class of languages is referred to as the regular languages. (You might also see them referred to as the rational or finite-state languages.)
Moreover, there are algorithms by which to translate from any one of these forms into any other. For example, there is an algorithm that, given a regular expression as input, produces a DFA that describes the same language.
Theorem 4.1: The class of regular languages is closed under the set theoretic operations of union, intersection, and complement, as well as the language theoretic operations of concatenation and Kleene/Star Closure.
As a corollary (see Example 4.1), regular languages are also closed under set difference, which can be expressed in terms of intersection and complement.
Proofs:
Closure under union: Let R and S be regular languages. It follows that there exist regular expressions r and s such that L(r) = R and L(s) = S (i.e., the language described by r (respectively, s) is R (resp., S)). Then the regular expression r + s describes R∪S, from which it follows that R∪S is itself regular.
Closure under concatenation: Follow the logic from the previous paragraph, but this time form the regular expression r · s, which describes R·S.
Closure under Kleene/Star closure: Let R be a regular language. It follows that there is a regular expression r such that L(r) = R. Then the regular expression r* describes R*, from which it follows that R* is itself regular.
Closure under complement: Unlike in the three proofs above, here using regular expressions is not helpful, because regular expressions have no complement operator. More generally, it is not at all clear how one could take a regular expression r describing language R and modify it to produce a regular expression describing Rc (the complement of R). (We use c as a superscript to denote complement.)
A much better approach is to make use of DFAs. Indeed, if a DFA M has state set Q and final state set F, then the DFA Mc that is identical to M, except that its final state set is Q−F, is such that L(M) and L(Mc) are complements of one another. In other words, changing each state's status from non-final to final, or vice versa, complements the language that a DFA accepts.
Note that this construction does not work in the realm of NFAs. As an exercise, it is left to the reader to figure out why.
x ∈ (Rc ∪ Sc)c
= < Complement, Non-member >
¬(x ∈ Rc ∪ Sc)
= < Union >
¬(x ∈ Rc ∨ x ∈ Sc)
= < DeMorgan (L2) >
¬(x ∈ Rc) ∧ ¬(x ∈ Sc)
= < Complement, Non-member (twice) >
¬(¬(x ∈ R)) ∧ ¬(¬(x ∈ S))
= < Double Negation (twice) >
(x ∈ R) ∧ (x ∈ S)
= < Intersection >
x ∈ R ∩ S
|
a proof of which is on the right. What this says is that if we take the union of the complements of R and S, and then take the complement of that language, we get the intersection of R and S. Because each applied operation preserves regularity, the resulting language is regular, assuming that both R and S are regular.
The proof just described is non-constructive, in the sense that it does not tell us how to take descriptions of regular languages R and S (e.g., as regular expressions or FA's) and build a description of R ∩ S.
Here is a constructive proof based upon DFA's.
Let Mi = (Qi,Σi,δi,
qi,0,Fi), i=1,2, be a pair of DFAs.
Then M = (Q,Σ,δ,q0,F) accepts
L(M1) ∩ L(M2), where
Q = Q1 × Q2,
Σ = Σ1 ∩ Σ2,
q0 = [q1,0,q2,0],
F = F1 × F2, and
for each [p,r] ∈ Q and a ∈ Σ,
δ([p,r],a) = [s,t], where s = δ1(p,a)
and t = δ2(r,a).
The vital property of this construction is this: For every string x∈Σ*, and all states p,s ∈ Q1 and r,t ∈ Q2:
Using the notation A ↝z B to mean that there is a sequence of transitions from state A to state B spelling out z, what the above says is that [p,r] ↝x [s,t] (in M) if and only if both p ↝x s (in M1) and r ↝x t (in M2).
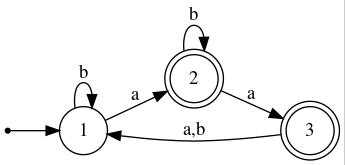
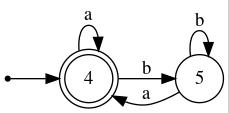
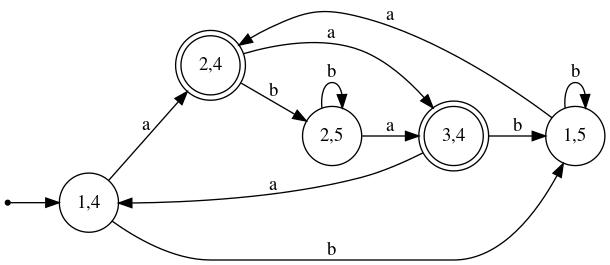
As an illustration of this so-called cross-product construction, see the figure below, in which two FA's are shown side-by-side and the result of performing the construction is shown underneath.
 |
 |

|
|
Theorem 4.2: The class of regular languages is closed under the language theoretic operation of reversal.
The reverse of a string is defined recursively as follows:
Base Cases: λrev = λ, arev = a (for a ∈ Σ)
Recursive Case: (a·x)rev = xrev·a (for a ∈ Σ, x ∈ Σ*)
For example, (aababbb)rev = bbbabaa
Extending the reverse operator in the natural way to apply to languages, we have, for L ⊂ Σ*,
To show that regular languages are closed under reversal, it suffices to show that, for any regular expression s, there exists a regular expression srev such that L(srev) = (L(s))rev (i.e., the language generated/described by srev is the reverse of that generated/described by s). A constructive proof would describe exactly how —via an algorithm— to obtain srev from s. That is what we do next.
Here is a set of equations that, in effect, describe a recursive algorithm by which to perform such a transformation. The first two equations correspond to the base cases; the remaining three are recursive/inductive cases. It is to be understood that r and s are regular expressions.
| ∅rev | = | ∅ | |
| arev | = | a | (for a ∈ Σ) |
| (r + s)rev | = | rrev + srev | |
| (r · s)rev | = | srev · rrev | |
| (r*)rev | = | (rrev)* |
Applying this construction to (abb + ccab)*·ba*c, we get ca*b · (bba + bacc)*
Theorem 4.3: The class of regular languages is closed under homomorphism. A homomorphism is a function that maps each symbol in an alphabet to a string in some (possibly different) alphabet. (E.g., h(0) = abb, h(1) = ba is a homomorphism from {0,1} into {a,b}*.)
Extending the definition of homomorphism in the natural way to apply to languages, we have, with respect to a homomorphism h whose domain is Σ and a language L ⊆ Σ*,
It is left to the reader to describe a construction by which to transform a regular expression r into a regular expression rh such that L(rh) = h(L(r)) (i.e., the language generated/described by rh is that obtained by applying h to the language generated/described by r).
Definition of Right Quotient: Let x and y be strings over some alphabet. Then xy/y = x is the right quotient of xy with y. If string v is not a suffix of string u, then u/v is undefined.
Extending the definition to languages in the usual way, we have
Theorem 4.4': Let L1 be a regular language and L2 be any (even possibly nonregular) language. Then L1/L2, the right quotient of L1 with L2, is a regular language.
This section addresses the issue of which problems regarding regular langauges have algorithmic solutions. Such problems are of the form
Given a regular language L (and possibly other stuff, such as a second language and/or a string), determine whether or not ...
Before we can even discuss how to solve such a problem, we need to know in what form the given language(s) is provided. An algorithm works on a "concrete representation" of whatever "inputs" it is given (even if we usually think of those inputs at a high level of abstraction). What concrete representation would a regular language take?
Answer: A DFA, NFA, regular expression, or regular (i.e., either right- or left-linear) grammar. Any of these will be suitable, as from any one of them we can algorithmically produce an equivalent of any of the other forms, as was demonstrated in Chapter 3.
Problem #1 (Membership): Given a regular language L and a string x, determine whether or not x is a member of L. (Theorem 4.5)
As a special case (see Exercise 4.2.7) of Problem #1, fix the input x to be λ. That is, the problem is to determine, for a given regular language, whether λ is a member. (Being a special case of a more general problem, it may have a simpler solution.)
Problem #2 (Finite vs. infinite): Given a regular language L, determine whether it is finite or infinite. (Theorem 4.6)
A special case of Problem #2 is this: Given a regular language L, determine whether L = ∅ (Being a special case of a more general problem, it may have a simpler solution.)
Another special case (see Exercise 4.2.8) of Problem #2 is this: Given a regular language L over alphabet Σ, determine whether L = Σ*. (Being a special case of a more general problem, it may have a simpler solution.)
Problem #3 (Language equality): Given regular languages L1 and L2, determine whether or not L1 = L2. (Theorem 4.7, p. 115)
Linz begins this section by proving, using the Pigeonhole Principle, that the language { anbn | n≥0 } is not regular. This is the "canonical" non-regular language, i.e., the language most commonly used as the first example of a non-regular language, probably because it is among the simplest such languages and easiest to prove non-regular.
Linz then goes on to state and prove the Pumping Lemma for Regular Languages, which describes a necessary condition for a language to be regular. Hence, any language failing to satisfy that condition must be non-regular.
The proof of the Pumping Lemma is, in effect, a generalization of the proof that { anbn | n≥0 } is not regular. Having showed that proof, he applies the lemma to that language (see Example 4.7), this time making for a very short proof of non-regularity.
Linz then goes on to use the lemma to show several more languages are non-regular in Examples 4.8-4.13. In Example 4.12 he uses closure under homomorphism to aid in making the proof simpler (specifically, by using a homomorphism that maps the given language into the canonical non-regular language).
In Example 4.13, he proves non-regularity twice, the first time using a clever application of the Pumping Lemma, the second time using closure properties to show that the regularity of the given language implies the regularity of the canonical non-regular language.