Odd # of b's
Examples 1 and 2: Our first example (below and to the left) is a finite state machine that recognizes the language
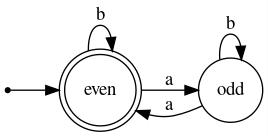
containing those strings over the alphabet {a,b} having an even number of occurrences of a. Two states suffice, as the only thing that the machine must "remember" while it "consumes" input symbols is the parity (evenness/oddness) of the number of a's it has read so far.
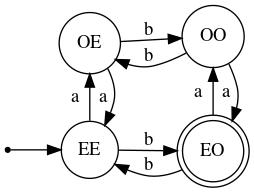
Below and to the right is shown a FSM that accepts a string over {a,b} iff it contains an even number of a's and an odd number of b's. That is, its language is
As does the first machine, this one must keep track of the parity of the number of a's read so far, but it must also do this for b's. Hence, four states are needed.

|

|
| Even # of a's | Even # of a's ∧ Odd # of b's |
|---|
Suppose that we were to relax the requirement from and to or; that is, suppose the machine was intended to accept any string having either an even number of a's or an odd number of b's. The only change necessary would be to make states OE and EE final/accepting (leaving OO as the only non-final state).
Example 3: The FSM below accepts precisely those strings (over {a,b}) in which every run of a's has even length. (A run is a substring in which every symbol is the same and that is bordered on each side by either a different symbol or a terminus of the string. For example, in the string aaaabbaab there are two runs of a's, one having length four and the other length two.)
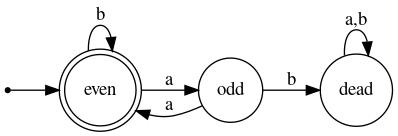 |
| All runs of a's have even length |
|---|
This machine keeps track of the parity of the number of a's it has consumed since the last occurrence of b (or since the beginning of the input string, if there have been no b's). However, if an odd-length run of a's is detected, the machine goes into a dead state.
Exercises: Modify the FSM shown above so that its language is
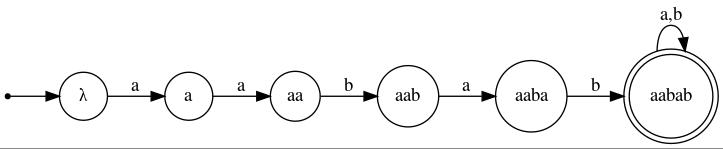
Example 4: Here we develop a DFA that accepts the language
First we begin with the DFA's spine, which is essentially a path from the initial state to a final state spelling out the string of interest:

|
Of course, once a computation has entered the final state, the string aabab has been encountered and thus the input string should be accepted, no matter what symbols follow. Thus, the final state should be made immortal:
|
What remains is to fill in the missing transitions, consistent with the intent that, if the machine is in a state named y, then y is the longest prefix of aabab that is also a suffix of the input read so far. For example, the outgoing transition labeled a from state aaba should go to state aa (and not all the way back to state λ, for example). Upon supplying the remaining transitions, we get
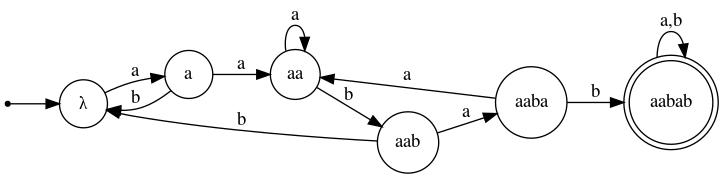
|
Rather than designing a DFA from scratch, it would have been easier to design an NFA (nondeterministic finite automaton) and then to apply the Subset Construction Algorithm by which to convert the NFA into a DFA that accepts the same language.
An NFA for this language could remain in its initial state until such time as it "guessed" that a particular occurrence of a in the input string was the first symbol in an occurrence of the "target" string, aabab. Here is that NFA:
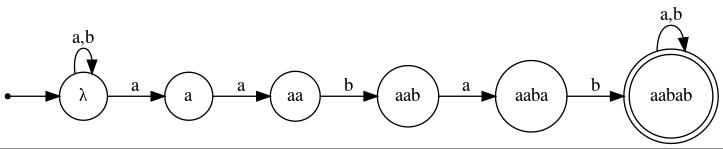
|
Example 5: Below is an NFA that accepts the language
In other words, the strings to be accepted are those in which a is the 3rd-to-last symbol. Upon receiving an a as input it "guesses" as to whether or not the input string will end two symbols later. A DFA accepting this language would need eight states, as it would need to "remember" the last three symbols it had read. (Initially, the machine could "pretend" that it had already read three b's, making it unnecessary for it to distinguish between whether, for example, the first input symbol were a or the first four input symbols were bbba.)
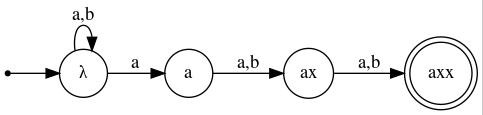
|
Suppose that the target language were changed to
for some constant k≥0. An NFA for this language can be obtained from the one shown above easily: just add new states and transitions so as to make the path from state a to the final state be of length k. The resulting machine would have k+1 states.
A DFA for such a language would require 2k+1 states, as it would have to "remember" the suffix of length k+1 of the input it had read so far.