(q1,aabbb,10) ⊦
(q1,abbb,110) ⊦
(q1,bbb,1110) ⊦
(q2,bb,110) ⊦
(q2,b,10) ⊦
(q2,λ,0) ⊦
(q3,λ,λ)
A PDA (pushdown automaton) has seven components:
The computation of a PDA is assumed to begin in its initial state with the stack containing a single symbol, its bottom-of-stack symbol. You can think of the bottom-of-stack symbol as a placeholder that makes it convenient for the machine to determine whether the stack is, logically speaking, empty.
The meaning of a transition is as follows: If (s,x) ∈ δ(p,a,b) (p,s ∈ Q, a∈Σ, b∈Γ, x ∈ Γ*) it means that the machine, when in state p and scanning input symbol a with symbol b at the top of the stack, can (as it consumes that input symbol) go to state s and replace b at the top of the stack by the string x.
In the case that a = λ it would mean that the described actions could occur, without consuming any input symbols, regardless of what the next input symbol (if any) was.
A computation is a sequence of configurations through which a PDA passes while processing an input string. A configuration is an ordered triple that shows the state that a PDA is in, the as-yet-unconsumed suffix of the input string, and the contents of the stack. For example, (p,aabbbb,110) depicts a PDA that is in state p, has yet to consume the input symbols aabbbb, and has 110 on its stack (left-to-right corresponds to top-to-bottom).
Linz, Example 7.2: Linz presents a PDA by describing it algebraically. For example, he writes
which means that the PDA can make either of two transitions that consume input symbol a when in state q0 with 0 at the top of the stack. One transition goes to state q1 and pushes a 1 onto the stack (corresponding to replacing 0 by 10); the other one goes to state q3 and pops the 0 off the stack (corresponding to replacing 0 by λ).
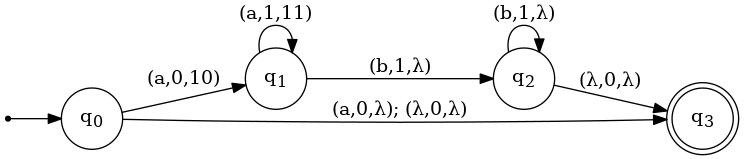
In Example 7.3/Figure 7.2, Linz shows a diagram of the PDA (which has 0 as its bottom-of-stack symbol). It appears on the left below; on the right is an accepting computation of that PDA on the input string aaabbb.

|
(q0,aaabbb,0) ⊦ (q1,aabbb,10) ⊦ (q1,abbb,110) ⊦ (q1,bbb,1110) ⊦ (q2,bb,110) ⊦ (q2,b,10) ⊦ (q2,λ,0) ⊦ (q3,λ,λ) |
The computation ends in a final state (q3) having consumed all of the input string. Hence, that string is deemed to be accepted by this PDA, which makes it a member of the language accepted by this PDA.
Suppose that the input string had been aaaabb. Had the machine made the same first move as in the computation shown above, it would have pushed four 1's onto the stack while consuming the a's in the input string, all the while in state q1. Then, as it consumed the two b's, it would have popped two 1's from the stack. At that point the machine would have been in configuration (q2,λ,110), from which there is no transition. Clearly, this example generalizes to every string of the form ajbk, where j>k, implying that no string of that form is accepted (with the exception of string a = a1b0, as discussed below).
Now suppose that the input string were aabbbb. Here, the machine would push two 1's onto the stack while consuming the two a's. Then, while consuming the first two b's it would have popped the two 1's from the stack, exposing the 0 at the botttom of the stack. That is, the machine would have reached the configuration (q2,bb,0), from which the only move is to q3, finishing with a configuration of (q3,bb,λ). Even though the machine "finishes" in a final state, this is not an "accepting computation" because not all of the input string was consumed. Clearly, this example generalizes to all strings of the form ajbk, where j<k, which implies that no string of that form is accepted.
Now suppose that the input string begins with b. The only possible first move is to go to q3 without consuming that b. Thus, the string is not accepted.
Finally, suppose that the input string begins with a but includes the substring ba. That is, it is of the form ajbkay, for some string y.
If j≥k, the machine will reach the (non-accepting) configuration (q2,ay,1j−k0), from which there is no transition.
If j<k, the machine will reach the configuration (q2,bk−jy,0), from which the only transition is to q3 (without the entire input string having been consumed, so it is not an accepting computation).
So far, our analysis has ignored the two transitions that go from q0 to q3. The transition labeled (a,0,λ) is relevant only if the input string happens to be a, and it allows that string to be accepted. It seems apparent that Linz's only reason for including this transistion was to illustrate the possibility of there being distinct transitions from a given state on the same (input symbol, top-of-stack symbol) pair. As for the transition labeled (λ,0,λ), it is for the purpose of allowing the empty string to be accepted.
From these observations and the analysis above, it should be clear that the presented PDA accepts the language {a} ∪ (anbn | n≥0 }.
Indeed, the "logic" of the machine is that, as it consumes a's it pushes 1's onto the stack to keep count (in unary notation, in effect), of how many a's it has read. As b's start being consumed, it pops the 1's from the stack so that, at any given, moment, the height of the stack (ignoring the 0 at the bottom) corresponds to the difference between the # of a's that were consumed and the # of b's that were consumed. If that difference ends up being zero, the string can be accepted. Otherwise it cannot be.
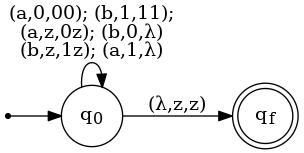
Linz: Example 7.4/Figure 7.3: Interestingly, even though the language accepted by the PDA in this example is more complex, the machine is perhaps simpler. That language is { w ∈ {a,b}* | na(w) = nb(w) }.
As in the previous example, the idea is that the stack keeps track of the difference between the # of a's and b's consumed so far. That only two states are needed, rather than four, as in the previous example, is because there is no need to enforce the rule that all a's must precede all b's. On the other hand, two stack symbols (in addition to the bottom-of-stack symbol) are needed to differentiate between the case when the number of a's consumed so far exceeds the # of b's and the opposite case. Specifically, when there are 0's on the stack, it means the former case applies; when the stack contains 1's, the latter case applies.
Here is the PDA, in diagram form, together with an accepting computation.
|
(q0,aabbbbabaa,z) ⊦ (q0,abbbbabaa,0z) ⊦ (q0,bbbbabaa,00z) ⊦ (q0,bbbabaa,0z) ⊦ (q0,bbabaa,z) ⊦ (q0,babaa,1z) ⊦ (q0,abaa,11z) ⊦ (q0,baa,1z) ⊦ (q0,aa,11z) ⊦ (q0,a,1z) ⊦ (q0,λ,z) ⊦ (qf,λ,z) |
Another example of a language for which there is a relatively simple PDA is the set of palindromes (over, say, the alphabet {a,b}).
....
{an b2n } (Linz, Exercise 7.1.1)
{an bm cn+m} (Linz, Exercise 7.1.6(c))
{an bn+m cm} (Linz, Exercise 7.1.6(c))
{an bm : n ≤ m ≤ 3n} (Linz, Exercise 7.1.6(f))
Deterministic PDA's...