During the exam period (until 6pm) you are not to communicate with anyone except the course instructor regarding the material on the exam. A Zoom meeting will be ongoing during the exam period, and you are expected to be in attendance with your video enabled until you finish. Violations of these rules may lead to nasty grade penalties, even course failure.
In more pleasant news, the exam is "open book", meaning that you are allowed to refer to the textbook, hand-written notes, and any web pages accessible via the course web page.
The exam has two parts, A and B, each with six problems. You will be graded upon your best six answers, but at least two of them are to come from Part B.
Submit each problem solution (to the "Final Exam" folder) in a separate file, as soon as you have finished it. (If you wish to submit an improved or corrected solution later, you may do so.) Name each file using the problem ID and your last name. For example, if your name were "Glorphead", your solution to problem A4 should be in a file named A4_Glorphead.zzz (where zzz is the appropriate extension). If you happen to place a solution in a "plain text" file, please keep each line of text to a maximum of 80 characters. If you want to submit a photograph of handwritten work, please insert it into a .docx (or other appropriate) file rather than sending the .jpg (or whatever) file directly.
A1. Present a DFA that accepts precisely those bit strings having at least one occurrence of 000 and such that there are no occurrences of 11 coming after the last occurrence of 000.
For example, 1101000101011010001010 should be accepted (because the last occurrence of 000 (in boldface) is not followed by any occurrences of 11) but 1101000101011010001001101 should not be accepted (because there is an occurrence of 11 coming after the last occurrence of 000, both in boldface).
Give meaningful names to your states. Here, one would expect such names to include bit strings indicating the most recently consumed input symbols. Describing the DFA in table form would be nice.
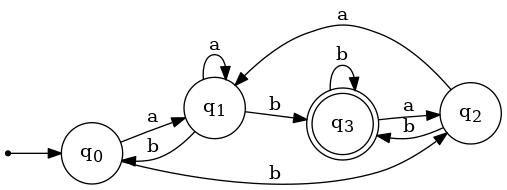
A2. Using the subset construction algorithm, present a DFA that accepts the same language as the NFA depicted below. The name of each state in your DFA should identify the set of NFA states from whence it came. Describing the DFA in table form would be nice.
| δ | Symbol | Transition Graph | |||
|---|---|---|---|---|---|
| Initial? | Final? | State | a | b |  |
| ✓ | q0 | {q1} | {q2} | ||
| q1 | {q1} | {q0,q3} | |||
| q2 | {q1} | {q3} | |||
| ✓ | q3 | {q2} | {q3} | ||
A3. Present a minimal DFA equivalent to the one shown below. Show the work you did to determine the equivalence classes of the state-indistinguishability relation. The name of each state in your DFA should identify the set of states from whence it came. Describing the DFA in table form would be nice.
| δ | Symbol | Transition Graph | |||
|---|---|---|---|---|---|
| Initial? | Final? | State | a | b | 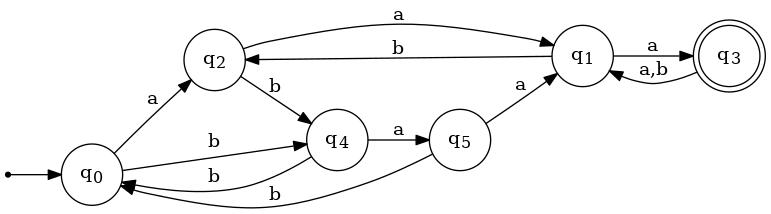 |
| ✓ | q0 | q2 | q4 | ||
| q1 | q3 | q2 | |||
| q2 | q1 | q4 | |||
| ✓ | q3 | q1 | q1 | ||
| q4 | q5 | q0 | |||
| q5 | q1 | q0 | |||
A4. Use your intuition to devise a regular expression that denotes the language accepted by the NFA shown below. Exploit the fact that the initial state is also the lone final state.
| δ | Symbol | Transition Graph | ||||
|---|---|---|---|---|---|---|
| Initial? | Final? | State | a | b | c | 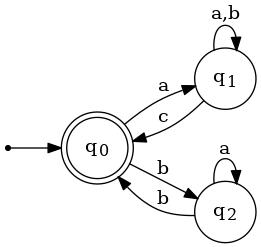 |
| ✓ | ✓ | q0 | q1 | q2 | ∅ | |
| q1 | q1 | q1 | q0 | |||
| q2 | q2 | q0 | ∅ | |||
A5. Present a CFG that generates the language {ambnapdnemcqfq | m,n,q≥0 ∧ p>0 }
A6. Describe, in a precise way, but without having to show the low-level details, a PDA that accepts the language described in the previous problem. Identify the states in such a machine and indicate each one's responsibility/role/purpose.
B7. Let G be a context-free grammar in Chomsky Normal Form, meaning that every production's right-hand side is either a single terminal symbol (as in A → b) or a pair of nonterminals/variables (as in A → BC). Prove by (strong) mathematical induction on |x| that the length of any derivation A ⟹+ x (where A is a nonterminal and x is a terminal string) is 2|x|−1. (The length of a derivation refers to the number of applications of productions.)
Hint: A leftmost derivation of a terminal string of length greater than one must have this form:
Apply the induction hypothesis to each of the "nested" derivations A ⇒+ x and B ⇒+ y.
B8. Define a Two-Shift Turing Machine to be one whose read-write head can move up to two cells to the left or right during a single transition, rather than being restricted to move by only one cell. Technically, such a machine's transition function would have signature
Show that every Two-Shift Turing machine can be simulated by a standard Turing machine.
A proper answer to this question would describe how to take an arbitrary Two-Shift TM M and produce from it a standard TM M' that simulates M. In particular, the description would need to address how M' would simulate a transition such as δ(p,a) = (q,b,RR) that causes the read-write head of M to move two cells to the right.
(a) Show that if S1 and S2 are countably infinite sets, so is their union S1 ∪ S2.
(b) (More difficult) Show that if S1 and S2 are countably infinite sets, so is their cartesian product
Hint: Recall our enumeration scheme for ℕ × ℕ.
Show that the class of recursive languages is closed under concatenation. That is, show that if L1 and L2 are recursive, so is
B11. A recursively enumerable (RE) language L is one for which there exists a membership procedure (i.e., one that, given a string x as input, will answer YES if x ∈ L and, otherwise, will either answer NO or never halt). Equivalently, an RE language is one such that there exists an enumeration procedure that, for each member of the language, will eventually "print" it (and will never print a string that is not a member of the language).
Let L1 be recursive and L2 recursively enumerable (RE). Show that L2 − L1 (i.e., { x | x ∈ L2 ∧ x ∉ L1 }) is necessarily RE.
B12.
Show that the class of functions of type ℕ ⟶ {true,false}
(i.e., functions that map each natural number to a boolean value)
is not countable.