| δ | ||||
|---|---|---|---|---|
| state | a | b | Initial? | Final? |
| 0 | 0 | 2 | ✓ | ✓ |
| 1 | 4 | 3 | ||
| 2 | 1 | 3 | ||
| 3 | 3 | 5 | ✓ | |
| 4 | 0 | 6 | ✓ | |
| 5 | 1 | 0 | ||
| 6 | 0 | 4 | ||
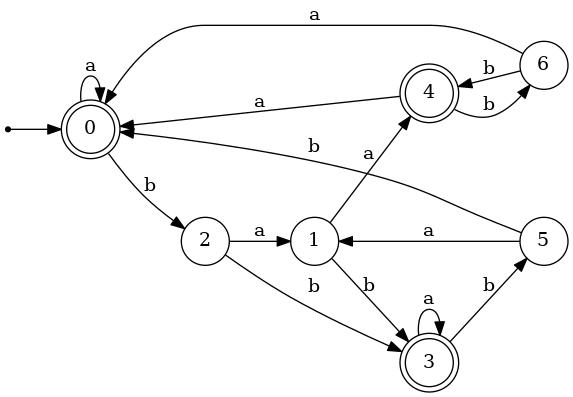
1. Apply the algorithm illustrated here to the DFA described below to minimize it. Show your work.
The names that you give to the states in the resulting DFA should make clear which set of states each one came from. For example, if you find that {0,3,4} is an equivalence class of the indistinguishability relation of the given DFA, the corresponding state in the minimized DFA should be named {0,3,4}.
|

|
|||||||||||||||||||||||||||||||||||||||||||
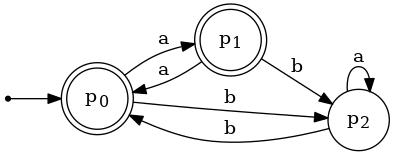
2. Pictured below are two DFA's, M1 and M2.
(a) Use the construction described in Linz's Theorem 4.1 to obtain a DFA that accepts L(M1) ∩ L(M2). (Describe it in table form, like the DFA in Problem 1. Make sure to name the states so that their connections to the states in M1 and M2 are obvious.)
(b) Describe the relatively minor modification that you would make to the DFA that was your answer to part (a) to get a DFA that accepts L(M1) ∪ L(M2) instead.
 |
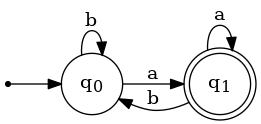 |
| M1 | M2 |
|---|
3. For a language L, define MAX(L) like this:
In words, MAX(L) is that subset of L containing those strings that cannot be extended to become longer members of L. Or, if you prefer, it contains every member of L that is not a proper prefix of any member of L.
Give a convincing argument that if L is a regular language, so is MAX(L).
Hint: Assume that L is given in the form of a DFA M and describe how to obtain a new DFA M' from M such that L(M') = MAX(L).
4. For a string x and a language L, define x-1L (the left quotient of L by x) as follows:
In words, x-1L is the set of strings obtained by chopping off the prefix x from every string in L that has x as a prefix.
Give a convincing argument that if L is a regular language and x is a string, x-1L is also a regular language.
Hint: Assume that L is given in the form of a DFA M and describe how to obtain a new DFA M' from M such that L(M') = x-1L.
5. The left quotient concept can be generalized so that both operands are languages, as opposed to one being a string and the other a language. Specifically, if L1 and L2 are languages,
In words, the language L1-1L2 contains precisely those strings that can be obtained by taking a string in L2 and chopping off a prefix that is a member of L1.
Give a convincing argument that if L2 is a regular language and L1 is any language, L1-1L2 is also a regular language.
Hint 1: Assume that L2 is given in the form of a DFA.
Hint 2: If you identify multiple states in a DFA as being
initial states, in effect you have described an NFA whose
initial state has a λ-transition to each of them.
6(a). Describe, informally, an algorithm to solve this problem:
Given a regular language L and a string x, determine whether L accepts any strings having x as a prefix.
(b) Describe, informally, an algorithm to solve this problem:
Given a regular language L and a string x, determine whether L accepts any strings having x as a substring.
7. Consider the language L = { akb2k | k≥0 }
(a) Use the Pumping Lemma to show that L is not regular.
(b) Theorem 4.3 in Linz shows that regular languages are closed under homomorphism. That is, if h is a homomorphism (i.e., a function that maps each symbol into a string, which naturally extends to be a function mapping strings to strings and then from languages to languages), then the regularity of L implies the regularity of h(L). What Linz does not show is that regular languages are also closed under inverse homomorphism, which is to say that the regularity of L implies the regularity of h-1(L) = { x | h(x) ∈ L }.
Thus, if for a given language L you identify a homomorphism h and a non-regular language L' such that L' = h-1(L), you will have shown L to be non-regular. Use this approach to show that L (as described at the beginning of this problem) is not regular. (Hint: The canonical non-regular language, { anbn | n≥0}, is useful here.)
8. Here is a q-grammar:
| S ⟶ | aAa | cB | (1) (2) |
| A ⟶ | bBa | λ | (3) (4) |
| B ⟶ | bSa | a | (5) (6) |
(a) Show the grammar's parse table.
(b) Using the parse table, show the "stack movie" illustrating the steps taken during a parse of the string abbcaaaa.
(c) Suppose that the grammar were augmented with the production S ⟶ λ. Is the resulting grammar a q-grammar? If it is, explain how the parse table from (a) would be updated to account for this new production. If it is not, explain why not.