CMPS 260 Spring 2022
Homework #4: Regular Expressions
Sample Solutions

Where r is a regular expression, L(r) denotes the language (i.e., set of strings) described by r.

1. Present a list containing precisely those strings of length six that are members of L( a(ba + c)^* ). Arrange the strings in alphabetical order.

Solution: a.ba.ba.c, a.ba.c.ba, a.ba.c.c.c, a.c.ba.ba, a.c.ba.c.c, a.c.c.ba.c, a.c.c.c.ba, a.c.c.c.c.c

2. Present a list containing precisely those strings of length five or less that are members of

Arrange the strings from shortest to longest; within each group of strings having the same length, put them in alphabetical order.

Solution:
Length 2: bb
Length 3: a.bb, bb.a
Length 4: a.a.bb, a.bb.a, ba.bb, bb.a.a bb.ab
Length 5: a.a.a.bb, a.a.bb.a, a.ba.bb, a.bb.a.a, a.bb.ab, ba.a.bb, ba.bb.a, bb.a.a.a, bb.a.ab, bb.ab.a

3. Present a regular expression describing L^R (the reverse of L), where L is the language described by the regular expression

Solution: (ba + a)* ab (bba + b)* (b + λ)

4. Present a regular expression r such that the language that it describes, L(r), is the complement of the language L, where

L contains precisely those strings having at least one a followed by an odd number of b's and is described by the regular expression aa^*b(bb)^*.

Solution #1: The complement of L includes string x ∈ {a,b}^* iff x satisfies at least one of the following properties:

• x has ba as a substring
• x has no occurrences of a
• x = aⁿb^2m for some n,m≥0

This observation gives rise to the regular expression (a+b)^*ba(a+b)^* + b^* + a^*(bb)^*

Solution #2: A different approach is to

1. devise a DFA for the given language,
2. complement that DFA (by changing each state's status from final to non-final or vice versa), and then
3. translate the resulting DFA into an equivalent regular expression.

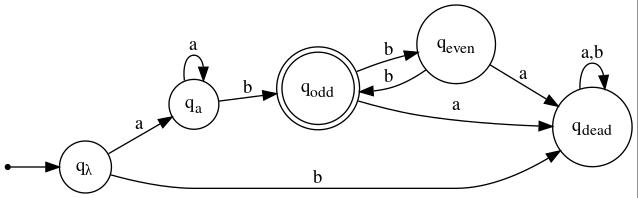
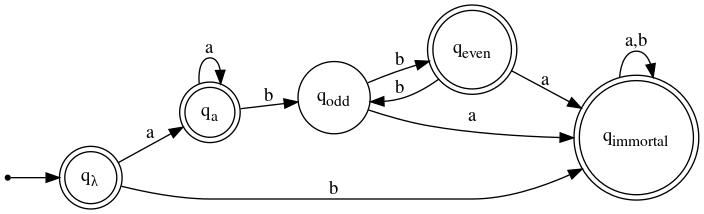
The DFAs that are the products of Step 1 and Step 2 are:

DFA for given language
DFA for its complement

To derive a regular expression describing the language accepted by the DFA that is the result of step 2, it will be useful to devise regular expressions r_λ, r_a, r_odd, and r_even such that, for q = q_λ, q_a, q_odd, and q_even:

In other words, L(r_q) is the set of strings that, starting in initial state q_λ, land you in state q.

Taking account of the fact that every state is final, except for q_odd, and that states q_λ, q_odd, and q_even have transitions to the immortal state labeled b, a, and a, respectively, a regular expression describing the language accepted by the DFA is

By examining the DFA, we observe that suitable regular expressions for r_λ, etc., are as follows:

rλ = λ

ra = a+

rodd = a+b(bb)*

reven = a+(bb)+

In an attempt to simplify r, we make the following observations:

Making use of these observations, we get

r	=	rλ  +  ra  +  reven  +  (rλ·b  +  (rodd  +  reven)·a)·(a+b)*
	=	λ  +  a+(bb)*  +  (b + a+b+a)·(a+b)*

This regular expression differs from the one derived in Solution #1, but they are equivalent.

5. Present a regular expression describing the language over {0,1} containing precisely those strings having exactly two occurrences of 11 and no occurrences of 111. As an aid, provided is the regular expression

describing the language over {0,1} containing precisely those strings having no occurrences of 11.

For a small bonus, present a second regular expression describing the language as described above, but allowing for the occurrence of 111. Such an occurrence counts as two overlapping occurrences of 11.

Solution: (10 + 0)^* 11 0(0 + 10)^* 11 (0 + 01)^*

Notice that the regular expression preceding the first occurrence of 11 (i.e., (10 + 0)^*) represents the set of strings that do not include 11 as a substring and are either empty or end with 0.

Similarly, the regular expression following the second occurrence of 11 (i.e., (0 + 01)^*) represents the set of strings that do not include 11 as a substring and are either empty or begin with 0.

The regular expression in between the two occurrences of 11 (i.e., 0(0 + 10)^*) represents the set of strings that do not include 11 as a substring and both begin and end with 0. An equivalent regular expression is (0 + 01)^*0

6. Present regular expressions for each of the following languages:

(a) { ba^2k  |  k≥0 }
Solution: b(aa)^*

(b) The set of strings over the alphabet {a,b} in which an even number of a's appear between any two occurrences of b.
Solution: a*(b(aa)*)*a*   (or a*(b + aa)*a*)

(c) { xby  |  x,y ∈ {a,c}^* ∧  n_a(y) is even }
Solution: (a+c)*b(c + ac*a)*

Reasoning: A common error made by students was to omit the c* in ac*a. Without it, a's must occur in adjacent pairs. But we want to allow any number of c's to occur between any pair of a's.

(d) The set of strings over the alphabet {a,b,c} in which an even number of a's appear between any two occurrences of b.
Solution: (a+c)*(b + c + ac*a)*(a+c)*

Reasoning: The (a+c)* factors at the beginning and end reflect the fact that any string over {a,c} can precede (respectively, follow) the first (respectively, last) occurrence of b. The (b + c + ac*a)* factor in the middle allows only (and all) strings over {a,b,c} in which every pair of b's has an even number of a's in between them.

(e) The set of strings over the alphabet {a,b,c} in which either

• an even number of a's appear between any two occurrences of b, or
• an even number of b's appear between any two occurrences of a

Reasoning: The first term is just the solution to (d) and the second term is the same as the first, with the roles of a and b interchanged.