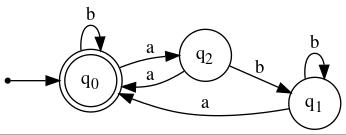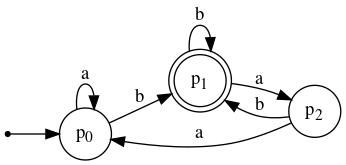
CMPS 260 Spring 2022
HW #5: Regular Languages, Closure Properties, Pumping Lemma
Due: 2pm, March 25

1. Pictured below are two DFA's, M₁ and M₂.

(a) Use the cross-product construction described in Linz's Theorem 4.1 (also see the web page pertaining to Linz's Chapter 4) to obtain a DFA that accepts L(M₁) ∩ L(M₂). (Describe it in table form, and make sure to name the states so that their connections to the states in M₁ and M₂ are obvious.) Feel free to show the transition graph, too.

(b) Describe the relatively minor modification that you would make to the DFA that was your answer to part (a) to get a DFA that accepts L(M₁) ∪ L(M₂).

(c) Describe the relatively minor modification that you would make to the DFA that was your answer to part (a) to get a DFA that accepts L(M₁) − L(M₂) (which is the same as L(M₁) ∩ (L(M₂))^c).

M1

M2

2. For a language L, define MAX(L) like this:

In words, MAX(L) is that subset of L containing those strings that cannot be extended to become longer members of L. Or, if you prefer, it contains every member of L that is not a proper prefix of any member of L.

Give a convincing argument that if L is a regular language, so is MAX(L).

Hint: Assume that L is given in the form of a DFA M and describe how to obtain a new DFA M' from M such that L(M') = MAX(L).

3. For a string x ∈ {a,b,c}^*, define ERASE*_a(x) to be the set of all strings obtainable from x by erasing zero or more occurrence of a. For example,

ERASE*a(baabcabacb)   =

{ baabcabacb,    babcabacb, baabcbacb, baabcabcb,    bbcabacb, babcbacb, babcabcb, baabcbcb,    bbcbacb, bbcabcb, babcbcb    bbcbcb }

Extending the definition to apply to languages, we have

That is, y ∈ ERASE*_a(L) iff y is the result of erasing zero or more occurrences of a from some x ∈ L.

Let L be a regular language over the alphabet {a,b,c} (or any other alphabet that includes a). Present two convincing arguments that ERASE*_a(L) is regular:

• One argument should assume that L is given in the form of a DFA M and describe how to obtain a new DFA (or, more likely, an NFA) M' from M such that L(M') = ERASE*_a(L). Suggested is a construction that makes use of λ-transitions.
• The other argument should assume that L is given in the form of a regular expression r and describe how to obtain a new regular expression r' such that L(r') = ERASE*_a(L). Suggested is a construction that makes use of the λ regular expression.

4. For a string x ∈ {a,b,c}^*, define ERASE1_a(x) to be the set of all strings obtainable from x by erasing exactly one occurrence of a. For example,

Note that the string obtained by erasing the first a is the same as that obtained by erasing the second. Similarly for the 5th and 6th occurrences of a. That explains why, even though aabcabacbaab has six occurrences of a, ERASE1(x) contains only four strings rather than six.

Extending the definition to apply to languages, we have

That is, y ∈ ERASE1_a(L) iff y is the result of erasing one occurrence of a from some x ∈ L.

Let L ⊆ {a,b,c}^* be a regular language. Make a convincing argument that ERASE1_a(L) is regular.

Hint: Assume that L is given in the form of a DFA M and describe how to obtain a new DFA (or NFA) M' from M such that L(M') = ERASE1_a(L). Suggested is a construction in which, for each (non-dead) state in M there are two states in M'. (After all, each state in M' needs to "know" whether or not an a already has been erased.)

5. (Challenging) Present a convincing argument that, if L is regular, so is the language

That is, x ∈ L' iff xx^rev ∈ L. For example, if abbabbabba (which is abbab·(abbab)^rev) were a member of L, then abbab would be a member of L'.

Hint: Assume that L is provided in the form of an NFA M = (Q, Σ, δ, q₀, {q_f}). (Without loss of generality, you may assume that M has exactly one final/accepting state, q_f.) Define δ^rev as follows: For every p,q ∈ Q and every a ∈ Σ:

In other words, δ^rev describes the same set of transitions as does δ, except that their directions are reversed.

Now let M^rev = (Q, Σ, δ^rev, q_f, {q₀}) be the NFA obtained from M by swapping the roles of its initial and final states and by reversing the direction of every transition. Note that L(M^rev) = L^rev (the reverse of L).

Now form M × M^rev (via the cross-product construction described in Linz's Theorem 4.1) The trick is in choosing the correct set of final states.

6. For each of the given decision problems, present a persuasive argument that it is decidable (i.e., there exists an algorithm that solves it). Typically, that would be done by describing such an algorithm, which could be expressed at a high level of abstraction. As examples, statements such as

• "Let state s = δ^*(q,x) (or, in the case of an NFA, let S be the set of states δ^*(q,x))",
• "Transform regular expression R into an equivalent DFA M",
• "Let DFA M be such that L(M) = L(M₁) ∪ L(M₂)", and
• "Let M' be identical to DFA M except that its initial state is δ^*(q₀,w) (i.e. the state reached from the initial state of M by following the transitions that spell out w)"

(a) Given a regular language L and a string x, determine whether any prefix of x is a member of L.

(b) Given a regular language L and a string x, determine whether any member of L has x as a suffix.

(c) Given a regular language L and a string x, determine whether any member of L has x as a substring.

7. Consider the language L = { a^kb^2k  |  k≥0 }

(a) Use the Pumping Lemma to show that L is not regular.

(b) The language { a^kb^k  |  k is even } is easily shown to be non-regular. Use that fact together with a closure property of regular languages to show that L is not regular.

8. (Optional bonus problem)
Identify a counterexample to the claim that if L is a regular language, then so is { xx^rev  |  x ∈ L }.