| δ | ||||
|---|---|---|---|---|
| state | a | b | Initial? | Final? |
| 0 | 0 | 2 | ✓ | ✓ |
| 1 | 4 | 3 | ||
| 2 | 1 | 3 | ||
| 3 | 3 | 5 | ✓ | |
| 4 | 0 | 6 | ✓ | |
| 5 | 1 | 0 | ||
| 6 | 0 | 4 | ||
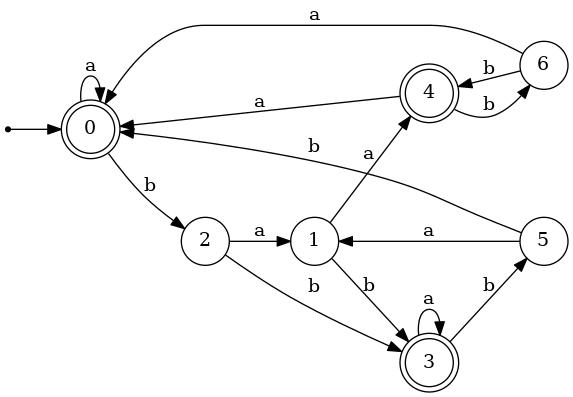
1. Apply the algorithm illustrated here to the DFA described below to minimize it. Show your work.
The names that you give to the states in the resulting DFA should make clear which set of states each one came from. For example, if you find that {0,3,4} is an equivalence class of the indistinguishability relation of the given DFA, the corresponding state in the minimized DFA should be named {0,3,4}.
|

|
|||||||||||||||||||||||||||||||||||||||||||
2. Provide a precise description of the language generated by this context-free grammar:
| S | ⟶ | aSb | M | (1) (2) |
| M | ⟶ | bbMa | c | (3) (4) |
Such a language description could be similar to those given in the next two problems.
3. Present a context-free grammar that generates the language { akbma2m+k | k,m ≥ 0 } ∪ { akb2mak | k≥0, m≥1 }
4. Present a context-free grammar that generates the language { 0m1n | 2m ≤ n ≤ 3m }
5. Apply the exhaustive parsing algorithm to determine whether or not bbaaaba ∈ L(G5), where G5 is this CFG:
| S | ⟶ | bSR | a | (1) (2) | |
| R | ⟶ | aRb | a | (3) (4) |
To illustrate the workings of the algorithm, show the breadth-first tree that it, in effect, traversed during its execution. (Each node of that tree is labeled by a sentential form.)
Your grammar should be such that derivation trees are consistent with the conventional operator precedence rules of regular expressions, which say that star has highest precedence, then concatenation, then union.
For example, a derivation tree for the regular expression a·b·b+b·a* should have one subtree correspoding to the subexpression a·b·b and another one corresponding to the subexpression b·a* (because + (union) has lower precedence than · (concatenation)). Within the latter should be a subtree corresponding to the subexpression a* (because the star operator —having higher precedence than concatenation— applies only to a, not to ba).
Hint: Compare the CFGs in Examples 5.11 and 5.12 of Linz, which are, respectively, ambiguous and unambiguous grammars for arithmetic expressions. Note that the CFG in Example 5.12 produces derivation trees whose structure reflects the usual rules of operator precedence (commonly referred to nowadays as "PEMDAS", unfortunately).
7. Let G be this q-grammar:
| S ⟶ | bDb | cE | (1) (2) |
| D ⟶ | cS | aEc | (3) (4) |
| E ⟶ | aSb | λ | (5) (6) |
(a) Show the grammar's parse table.
(b) Show the "stack movie" illustrating the steps taken during a parse —guided by the parse table from (a)— of the string baacbcb
(c) Let Gc be the grammar resulting from augmenting G by adding production (7): S ⟶ λ. Show that Gc is not a q-grammar. Do so by showing a pair of "successful" stack movies, in one of which production (1) is applied and in the other of which production (7) is applied in the "same circumstance" (i.e., with S at the top of the lower stack and b at the top of the upper stack).
(d) Let Gd be the grammar resulting from augmenting G by adding production (7): D → λ. Is Gd a q-grammar? If it is, explain how the parse table from (a) would be updated to account for this new production. If it is not, explain why not.
(e) (more difficult) Let Ge be the grammar resulting from replacing production (1) in G by the production (1') S → bDa. Show that Ge is not a q-grammar.